有向無環圖 (Directed Acyclic Graph, DAG) 指的是從點出發用有方向的箭頭連接到其他的點構成的整個圖，而且從任意點出發，不會回到自己本身 (無環)。

前面的文章所使用的各種流程圖的表達，都有使用到有向無環圖，比方說 PERT 圖、CPM 圖就是有向無環圖。

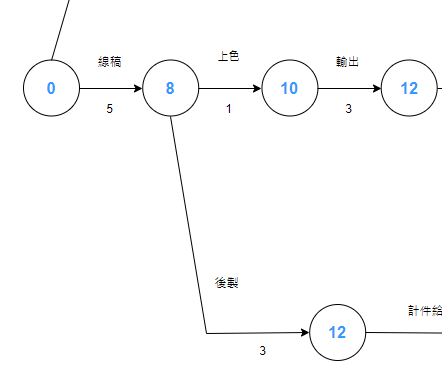
有向無環圖有很多種排列顯示的方式，比方說常見的這種是一般的有向無環圖畫法:

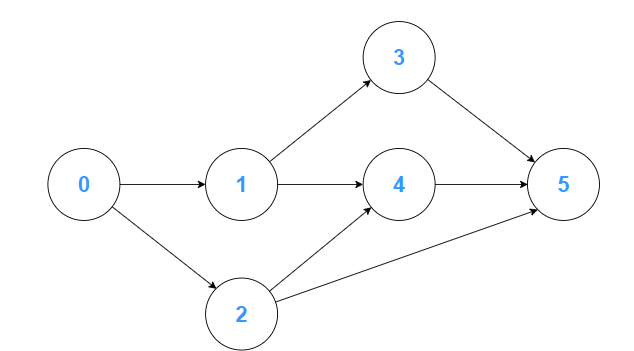
按照順序連接不同的點，也可以分出來，排法位置沒有很固定。

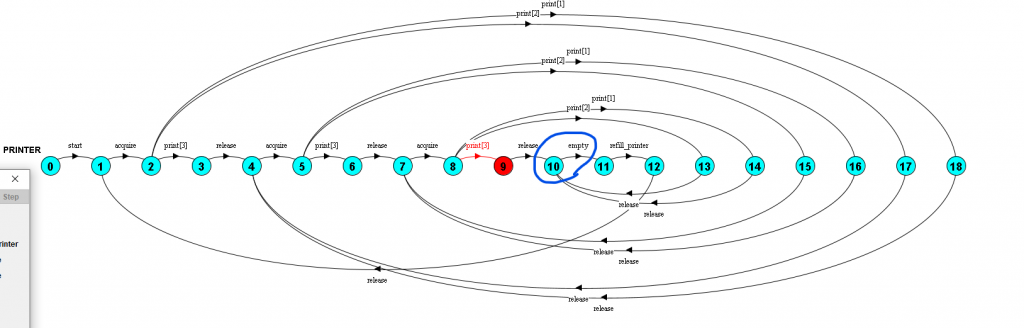
事實上之前的文章在介紹【有限狀態過程】，並不是一個 DAG，主要的原因是因為流程圖已經構成一個循環，會在後面的狀態回到自己，如下圖:

拓樸排序

拓樸排序，對於 DAG 來說，DAG 必有存在拓樸排序，若且唯若一個拓樸排序也是一個 DAG。

要展現【拓樸排序】的畫法，就需要讓箭頭被連結出去的數字呈現大小關係，下一項要大於前一項，然後畫出箭頭指向，假設以修課的範例來說，

假設三個課程模組: 0,1,2 以及 3 以及 4,5 ，有預備先修的課程關係: 要修 3 的話要先過 1，要修 4 的話要先過 2 ，這樣的修課關係可以變成像是下圖:

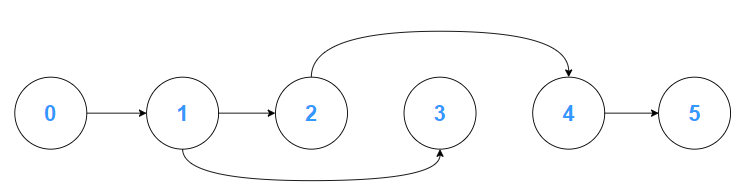
完全打平的結構，似乎較能呈現拓樸排序後直覺的結果。

其他有向無環圖結構

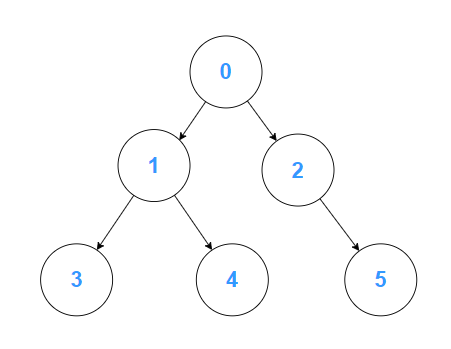
有向無環圖也可以用來表示樹的結構 (二元樹、多重樹)

另外參考到 [2] 的範例圖中也用了有向無環圖來表示數字的整除關係，叫做哈斯圖:

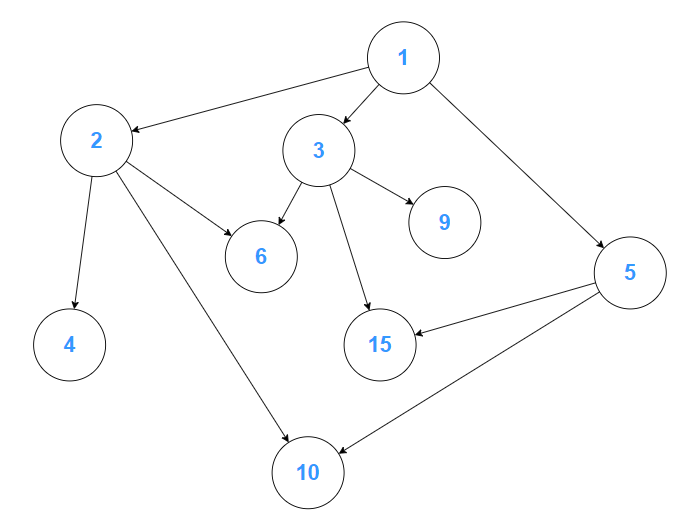
從一個只有 { 1, 2, 3, 4, 5, 6, 9, 10, 15 } 的集合中，要找出他們之前被整除的關係，這裡被 1 連結的，代表他們只能被 1 整除，前面的其他元素都無法整除他，也就呈現了質數的關係；

而後續的元素 4, 6, 9, 10, 15 都可以各自被 1 所連結到的元素整除，以此類推，這樣就構成了一個哈斯圖，哈斯圖的詳細應用及作法可以參考 [3]。

有向無環圖可以出現在任何地方，流程圖、區塊鏈 [4][5]、演算法、數學圖論，本篇文章也把幾個過去使用到有向無環圖都拿出來回顧了。

References:
[1] https://web.ntnu.edu.tw/~algo/DirectedAcyclicGraph.html
[2] https://zh.wikipedia.org/wiki/%E5%93%88%E6%96%AF%E5%9C%96
[3] https://blog.csdn.net/shulianghan/article/details/109061220
[4] https://www.chainnews.com/zh-hant/articles/767903222939.htm
[5] https://www.8btc.com/media/523587